The Mathematical Symphony of Bitcoin: How Equations Forged a Digital Revolution
The Math Never Lies
In the autumn of 2008, as the global financial system teetered on the brink of collapse—banks crumbling like ancient ruins under the weight of their own greed—a pseudonymous figure named Satoshi Nakamoto unveiled a nine-page manifesto that would reshape the world. Titled "Bitcoin: A Peer-to-Peer Electronic Cash System," this whitepaper was no mere technical blueprint; it was a mathematical elegy, a defiant proclamation that trust could be engineered not through human institutions but through the immutable laws of numbers. Bitcoin, the cryptocurrency it birthed, now commands a market worth trillions, powering everything from remittances in war-torn regions to operating companies all over the world actively stacking it on their balance sheets. Yet beneath its often talked-about volatility lies a bedrock of mathematical principles, elegant and unyielding, that safeguard its integrity against fraud, censorship, and the caprices of central authority.
Nakamoto drew upon cryptography, probability, and game theory to create a system where strangers could transact without intermediaries. These principles, often abstract and arcane, form the invisible scaffolding of Bitcoin. In the paragraphs that follow, we delve into each one, demystifying their intricacies with definitions, examples, and analogies drawn from everyday life. Imagine, if you will, Bitcoin not as code but as a grand architectural feat: a towering edifice built on mathematical pillars, each one load-bearing and indispensable. We begin at the foundation, ascending through the structure that has withstood over a decade of assaults, from hackers to governments.
Digital Signatures: The Invisible Ink of Ownership
At the heart of Bitcoin's transaction system beats the pulse of digital signatures, a cryptographic marvel that ensures only the rightful owner can spend their digital coins. Think of it as a seal on a medieval scroll: once affixed, it proves authorship and prevents tampering, but unlike wax and stamp, it's forged in the ether of mathematics.
A digital signature is a mathematical scheme for verifying the authenticity and integrity of a message or document. It relies on public-key cryptography, a duo of keys: a private key, known only to the owner (like a secret passphrase to a hidden vault), and a public key, shared with the world (akin to the vault's address on a public map). To sign a transaction—say, sending 1 Bitcoin to a friend—you use your private key to generate a unique signature based on the transaction details. Anyone can then use your public key to verify that the signature matches, confirming you authorized it without revealing the private key.
In Bitcoin, this is implemented using the Elliptic Curve Digital Signature Algorithm (ECDSA), which employs elliptic curve cryptography. Elliptic curves are mathematical functions shaped like gentle hills on a graph, defined by equations such as y² = x³ + ax + b. The "curve" allows for secure key generation with smaller numbers than traditional methods, making it efficient for computers. For example, multiplying a point on the curve by a large number (your private key) yields another point (your public key), but reversing this—finding the multiplier from the result—is computationally infeasible, like trying to “unbake” a cake to retrieve the original eggs and flour.
Picture a real-world analogy: You're at an auction house bidding on a priceless painting. Instead of shouting your bid, you whisper it to a trusted aide who announces it with a unique flourish only you two know—a twirl of the hand, perhaps. Bidders verify it's from you by recognizing the flourish, but no one can forge it without your secret. In Bitcoin, this prevents "double-spending," where someone tries to spend the same coin twice. The whitepaper notes: "Digital signatures provide part of the solution, but the main benefits are lost if a trusted third party is still required to prevent double-spending." Without them, Bitcoin would collapse into chaos, like a marketplace where counterfeit bills flow unchecked.
To illustrate, consider a simple transaction: Alice owns a Bitcoin output (a "coin") linked to her public key. She creates a new transaction outputting to Bob's public key, signs it with her private key, and broadcasts it. The network verifies the signature, ensuring Alice's consent. If Eve tries to forge it, lacking Alice's private key, her attempt fails spectacularly—the math doesn't lie.
Hash Functions: The Digital Fingerprint That Never Lies
If digital signatures are the seal, hash functions are the unbreakable chain binding Bitcoin's ledger together. These are one-way mathematical transformations that take any input—a sentence, a number, an entire novel—and produce a fixed-length output, called a hash, that appears utterly random. Crucially, the same input always yields the same hash, but even a tiny change flips the output dramatically, like a butterfly's wing altering a hurricane's path.
In cryptographic terms, a hash function must be collision-resistant (hard to find two inputs with the same output), preimage-resistant (impossible to reverse-engineer the input from the hash), and deterministic. Bitcoin uses SHA-256, part of the Secure Hash Algorithm family, which outputs 256 bits (64 hexadecimal characters). For instance, hashing "Hello, world!" might give "ed076287532e86365e841e92bfc50d8c," but changing it to "Hello, worlds!" yields something entirely different, like "f8e8b9f4a8b0e6d0c2f1b7e5a3d9c1b2."
The whitepaper describes: "The network timestamps transactions by hashing them into an ongoing chain of hash-based proof-of-work, forming a record that cannot be changed without redoing the proof-of-work." Here, hashes link blocks in the blockchain: Each block contains the hash of the previous one, creating an immutable sequence. Alter one transaction in an old block, and its hash changes, cascading through all subsequent blocks—like pulling a thread that unravels an entire tapestry.
Imagine a library where books are cataloged by fingerprints. Each book's fingerprint is unique; smudge a page, and the print changes. To forge a book, you'd need to recreate not just it but every linked volume afterward. In Bitcoin, this secures history: Miners compete to find hashes, but rewriting the past demands Herculean computation.
Proof-of-Work: The Laborious Lottery Securing the Network
Proof-of-work elevates hashing from mere fingerprinting to a competitive ordeal, akin to miners chiseling through digital rock to unearth virtual gold. It's the mechanism that decentralizes trust, forcing participants to expend real-world energy to validate transactions and add blocks.
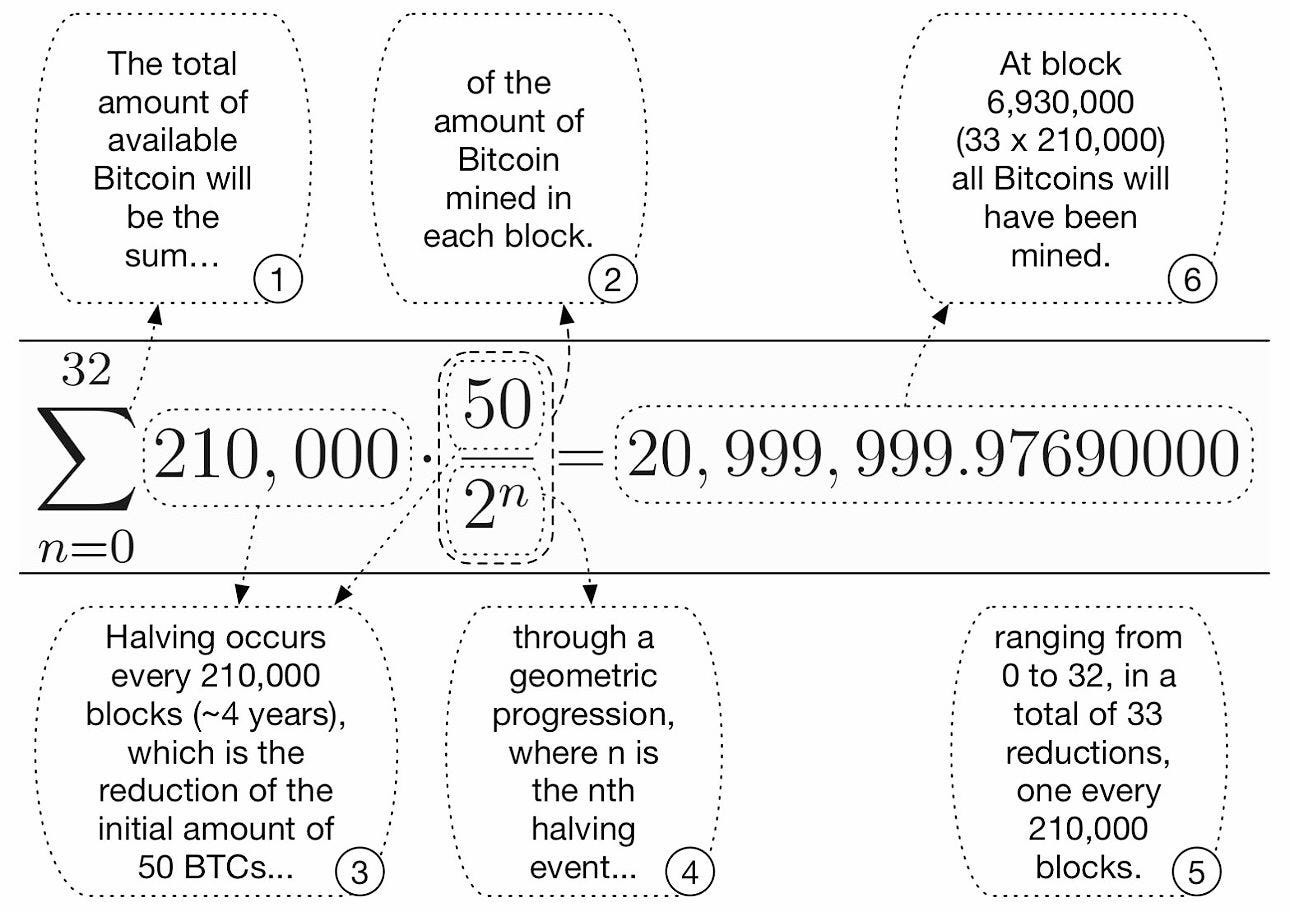
Defined in the whitepaper: "The proof-of-work involves scanning for a value that when hashed, such as with SHA-256, the hash begins with a number of zero bits." This "nonce" is a number miners guess repeatedly until the block header's hash meets the criterion—say, starting with 20 zeros. The difficulty adjusts every 2016 blocks to maintain a 10-minute average block time, based on network hash rate.
Mathematically, it's a probabilistic puzzle: The probability of success per guess is 1 over the target (a huge number), making it like winning a lottery where tickets cost electricity. The whitepaper likens it to Adam Back's Hashcash, originally for anti-spam emails.
One can consider a vast puzzle contest where entrants must find a combination that unlocks a box, but each try requires pedaling a bike generator. The first to succeed claims the prize and adds their puzzle piece to a growing chain. Cheating? You'd need to out-pedal everyone else combined. In Bitcoin, this prevents sybil attacks (fake identities flooding the network) and ensures the longest chain—requiring the most work—wins consensus. If an attacker with 30% of hash power tries to fork the chain, probability favors the honest 70%.
Merkle Trees: The Efficient Arbor of Verification
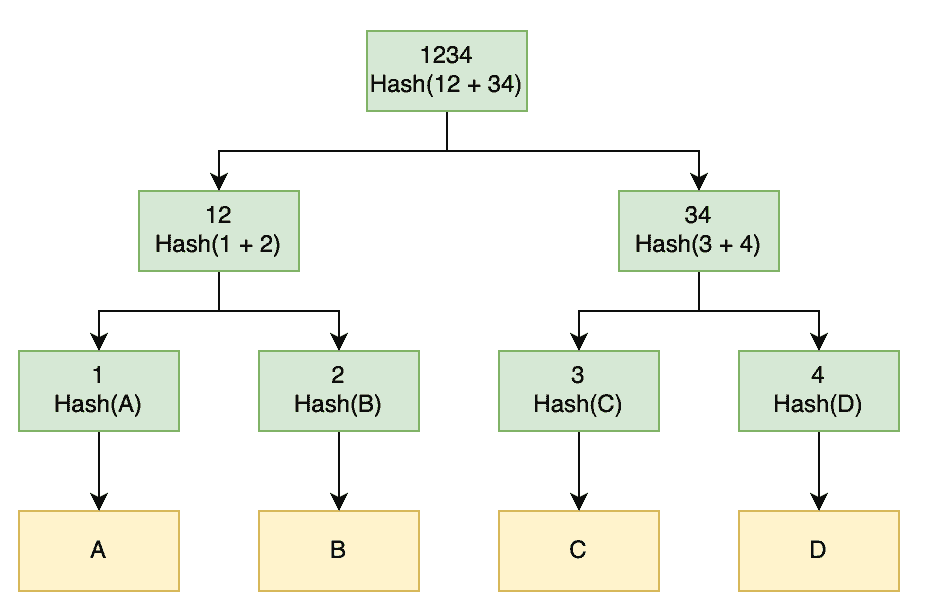
Amid Bitcoin's data deluge, Merkle trees stand as elegant organizers, compressing thousands of transactions into a single root hash for swift verification. Named after Ralph Merkle, it's a binary tree where leaves are transaction hashes, and parent nodes are hashes of their children.
The whitepaper explains: "To facilitate this without breaking the block's hash, transactions are hashed in a Merkle Tree, with only the root included in the block's hash." This allows "simplified payment verification" (SPV) for light clients, who check inclusion without downloading the full blockchain.
But how? Start with transaction hashes as leaves. Pair them, hash the pairs to form branches, repeat until the root. To prove a transaction exists, provide the path of hashes to the root—logarithmic in size, efficient like climbing a family tree with shortcuts.
For example (for the more mathematically inclined), four transactions A, B, C, D: Hash(A+B) = E, Hash(C+D) = F, Hash(E+F) = Root. To verify A, supply Hash(B) and F; recompute and match the root.
For the not so mathematically inclined, consider a corporate org chart where the CEO's summary encapsulates all departments. To check a lowly employee's report, you don't need every file—just the summaries up the chain. This prunes old data, reclaiming disk space while preserving integrity.
Probability Calculations: The Odds Against Deception
Bitcoin's security isn't absolute but probabilistic, a calculated gamble where math tilts the scales toward honesty. The whitepaper devotes a section to this, modeling double-spend attacks as statistical races.
Broadly, probability calculations assess risks using distributions and walks. Key: The chance an attacker reverses a transaction drops exponentially with confirmations (blocks added atop it).
Binomial Random Walk: The Step-by-Step Duel
As a subset of probability theory, the binomial random walk models the competition between blockchain chains as a series of steps along a path, where each step forward (+1) represents the addition of an honest block and each step backward (-1) signifies an attacker block, governed by probabilities p for an honest win and q equal to 1 minus p. The Bitcoin whitepaper describes this dynamic succinctly: "The race between the honest chain and an attacker chain can be characterized as a Binomial Random Walk," in which success for the honest side widens the lead while failure allows the attacker to narrow it. In this framework, each trial—corresponding to a block time—is independent and binomial, limited to just two possible outcomes, and over numerous steps, the process resembles a drunkard's stagger, tending toward the mean but still permitting extreme deviations due to chance.
For instance, if p equals 0.6, reflecting an honest majority, the expected lead after 10 steps would be 2, though variance introduces fluctuations; in the Bitcoin context, this illustrates how attackers typically fall behind unless q exceeds 0.5. To make it relatable, imagine two hikers racing up a mountain, with one being faster to represent the honest chain: each minute, the leader either advances further or the pursuer closes the gap slightly, and the mathematics predicts that the leader's victory becomes increasingly certain as the distance grows.
Poisson Distribution: Modeling the Attacker's Pace
For continuous time modeling in the Bitcoin whitepaper, the system employs the Poisson distribution to represent the attacker's potential progress, described as having an expected value λ equal to z multiplied by q over p, where z signifies the deficit in blocks. This distribution is particularly suited for modeling rare events, such as the discovery of blocks, with its mean given by λ, and the probability of exactly k events occurring calculated through the formula e to the power of negative λ, times λ to the power of k, divided by k factorial. It serves as an approximation to the binomial distribution in scenarios involving a large number of trials n and a small probability p, treating blocks here as discrete "events" unfolding over time.
For instance, if the deficit z is 6 and the ratio q over p is 0.1, then λ becomes 0.6, and the probability that the attacker catches up is determined by summing adjusted Poisson probabilities across possible values of k. To make this clearer, imagine raindrops hitting a window during a storm: the Poisson distribution predicts the number of drops in a given minute, much like how it forecasts the number of blocks an attacker might find while the honest chain continues to advance in Bitcoin's network.
Gambler's Ruin Problem: The Exponential Decay of Hope
Finally, the whitepaper draws an analogy to the Gambler's Ruin problem, stating that "the probability of an attacker catching up from a given deficit is analogous to a Gambler's Ruin problem." In this classic scenario, two players engage in a series of bets until one is completely ruined, with the probability of ruin for the underdog calculated as (q/p)^z if q is less than p, or 1 otherwise. It involves finite resources and biased coin flips, where the odds of ruin for the poorer gambler drop sharply as the disparity in their stakes grows.
For instance, if an attacker begins z blocks behind in a deficit, with q at 0.1 and p at 0.9, the probability of catching up becomes (0.1/0.9)^z, which is minuscule for z equal to 6—around 10^{-7}. This is much like a poker game where you start with just $10 against an opponent's $90, and the house edge works against you; the mathematics inevitably dooms the underdog, just as Bitcoin's accumulating confirmations probabilistically bankrupt potential attackers.
These principles intertwine, creating a system as resilient as a coral reef—each math concept a polyp contributing to the whole. From signatures proving ownership to probabilities quantifying trust, Nakamoto's whitepaper orchestrated a new monetary system bound by mathematical principles rather than human laws. In an era of eroding faith in institutions, Bitcoin reminds us: Numbers, unyielding and universal, can forge a new order. As markets ebb and flow, this mathematical symphony plays on, a testament to human ingenuity encoded in equations.
Thanks for reading and letting me nerd out on math.